Modified Nodal Analysis with Eigen
In a previous entry I described some experiments using a newly announced open-source numeric integration library called odeint. In the meantime it has been accepted into Boost and I’ve learned just enough about linear algebra to follow up my comment from the end:
The next logical step would be to take an arbitrary RC network, apply KCL, rearrange the resulting equations to isolate dx/dt, and thus automatically produce a model suitable for use with odeint
It turns out that there is a well-known procedure called Modified Nodal Analysis that maps circuit elements into a pair of matrices representing the system of equations that needs to be solved. Using this procedure, any circuit can be automatically turned into its equivalent matrix form. Here’s how this works in a simple RLC tank circuit:
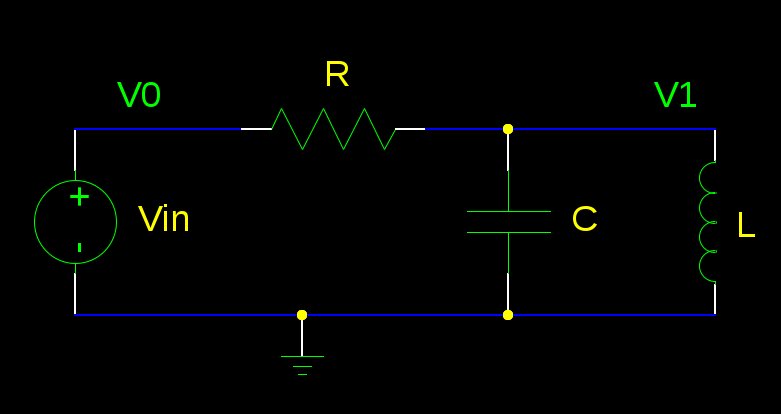
We can write two equations representing KCL for the input and output circuit nodes, and another two to represent the input source’s current and the current through the inductive load, to get four equations in four unknowns (our state variables):
\[\begin{array}{rcll} \frac{V_0-V_1}{R} + I_{in} & = & 0 & \mbox{from KCL} \\ \frac{V_1-V_0}{R} + C\frac{dV_1}{dt} + I_L & = & 0 \\ V_0 & = & V_{in} & \mbox{from independent source} \\ V_1 & = & L\frac{dI_L}{dt} & \mbox{from inductor} \end{array}\]Separating the coefficients of the voltage and current time derivatives and rewriting in matrix form produces:
\[\begin{multline*} \begin{bmatrix} 0 & 0 & 0 & 0 \\ 0 & C & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & -L \end{bmatrix} * \begin{bmatrix} \dot{V_0} \\ \dot{V_1} \\ \dot{I_{in}} \\ \dot{I_L} \end{bmatrix} + \begin{bmatrix} \frac{1}{R} & - \frac{1}{R} & 1 & 0 \\ - \frac{1}{R} & \frac{1}{R} & 0 & 1 \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} * \begin{bmatrix} V_0 \\ V_1 \\ I_{in} \\ I_L \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \\ V_{in}(t) \\ 0 \end{bmatrix} \end{multline*}\]You can see that each component type produces a characteristic stamp within the susceptance or conductance arrays, at the rows and columns corresponding to their connecting nodes. Values from additional components are simply summed if they overlap. This is the heart of MNA.
Now all that remains is to rewrite this equation so that each first derivative term is alone in its own row - or looked at another way, that the susceptance array is the identity matrix. This is evidently the same thing as “solving” the system of equations. Several open-source linear algebra libraries are available to do this work; I happened to choose Eigen due to its friendly reputation and also because it had the exact code I needed in one of its tutorial examples. The resulting code produced exactly the same results, but now has fewer lines and is implemented in a more general way. You can find it here.
I can now see a path to extending it for larger networks, perhaps reading from a file - SPEF parser, anyone? Also, the MNA representation allows for further processing - if I get ambitious I may try to implement some well-known Model Order Reduction algorithms, or do some graph processing (locating disconnected nets or resistive loops in the data).